Wskazy, wykresy wskazowe lub fazory nie brzmią jak najbardziej ekscytujące tematy, ale zaufaj mi — są bardzo użyteczne! Wskazy są obiektami matematycznymi, które są powszechnie używane w elektrotechnice i innych dziedzinach, które zajmują się zjawiskami falowymi takich jak optyka i akustyka.
Pojęcie wskazu zostało po raz pierwszy wprowadzone w XIX wieku przez Jamesa Clerka Maxwella, który użył go do wyjaśnienia zachowania obwodów prądu przemiennego. W obwodach tych napięcie i prąd stale się zmieniają, co utrudnia analizę ich zachowania przy pomocy tradycyjnych metod, stosowanych dla prądu stałego. Z tego powodu ludzkość musiała wynaleźć skuteczniejsze metody, które ułatwiłyby analizę obwodów prądu przemiennego.

Czym są wskazy ?
W dzisiejszej elektrotechnice fazory są używane do reprezentowania sygnałów elektrycznych oraz zależności między nimi w obwodach prądu przemiennego (AC). W praktyce najczęściej mamy do czynienia z harmonicznymi sygnałami przemiennymi, czyli takimi, które mogą być opisane za pomocą funkcji sinus bądź cosinus. Przykładem sygnału harmonicznego może być sygnał napięcia opisany zależnością:
$$u(t) = U_0\cos{\left(\omega t + \varphi\right)}$$
gdzie \(U_0\) jest amplitudą przebiegu, \(\omega\) jest pulsacją i jest proporcjonalna do częstotliwości \(f\) sygnału przemiennego \(\omega = 2\pi f\), a \(\varphi\) jest jego fazą początkową.
Wskazem zależnym od czasu lub amplitudą zespoloną:
$$u = \frac{U_0}{\sqrt{2}} e^{j(\omega t + \varphi)}$$
reprezentującym powyższy sygnał harmoniczny, będziemy nazywać liczbę zespoloną, której moduł jest równy amplitudzie \(U_0\) tego sygnału oraz której argument jest równy jego globalnej fazie: \(\omega t + \varphi\). Wskaz jest zatem najprościej otrzymać, wykorzystując postać wykładniczą liczby zespolonej.
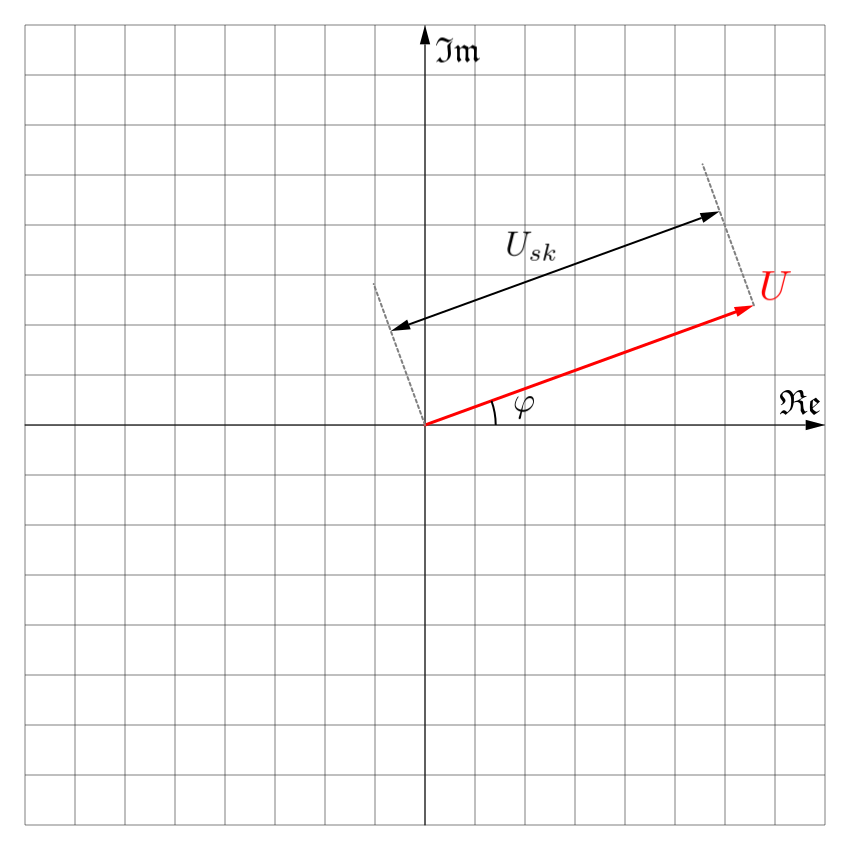
Aby zwizualizować wskaz, wyobraź sobie strzałkę wektora zaczepioną w punkcje \(0+j0\) płaszczyzny zespolonej. Długość wektora reprezentuje amplitudę \(U_0\) sygnału harmonicznego a jego kierunek względem osi rzeczywistej globalną fazę sygnału \(\omega t + \varphi\). Wraz z upływem czasu taki wektor będzie rotował wokół punktu zaczepienia z prędkością kątową równą \(\omega\) (zwykle wyrażoną w radianach na sekundę).
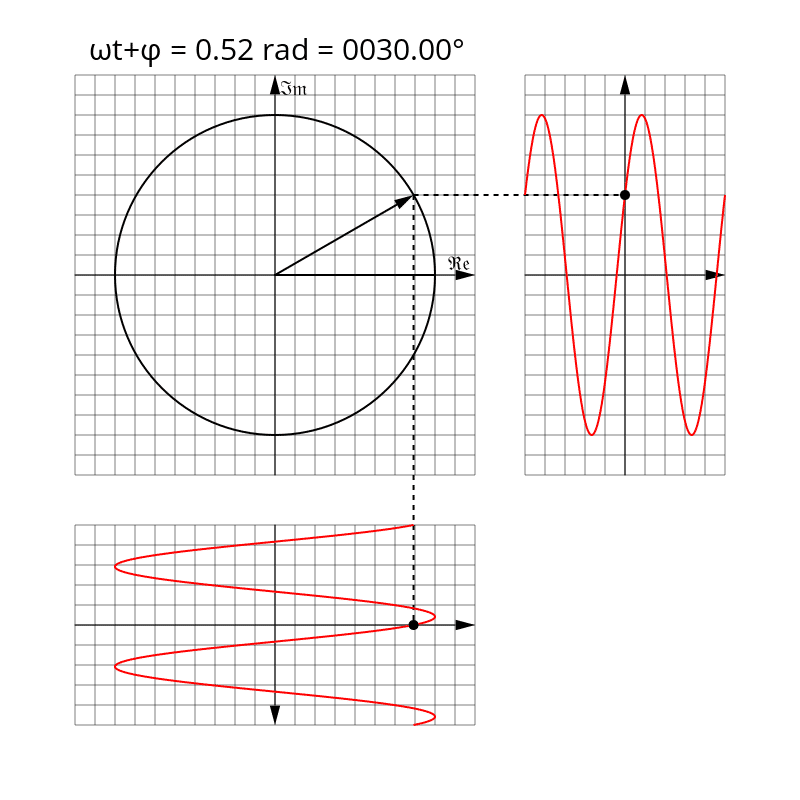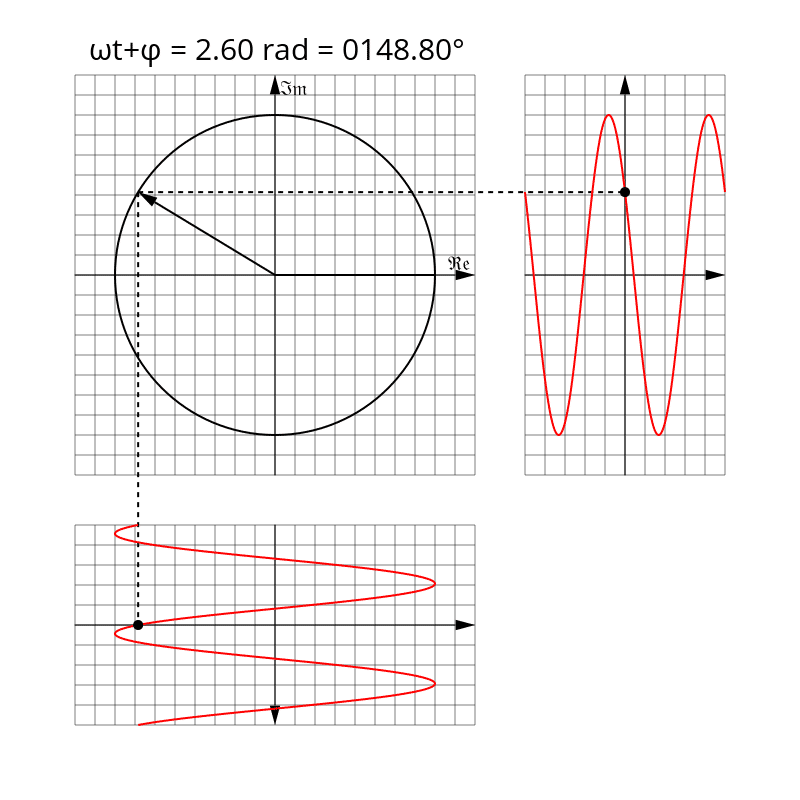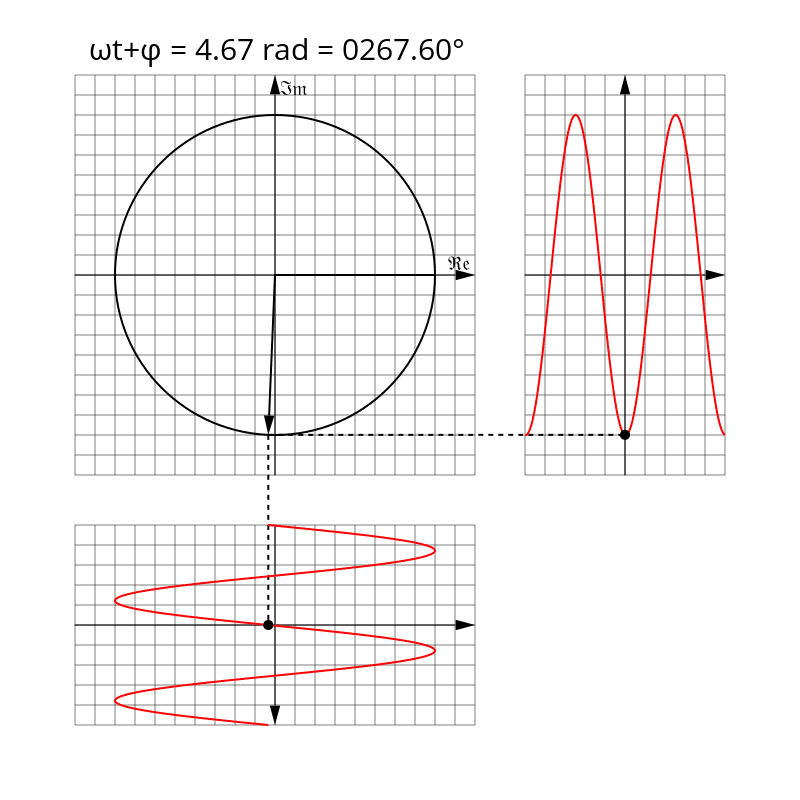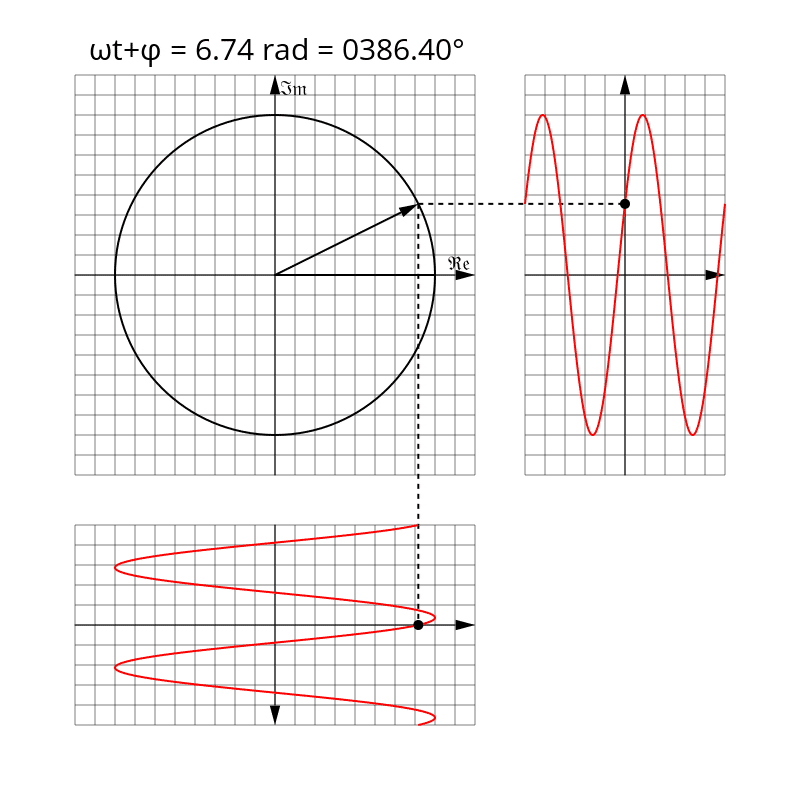
W obwodach prądu przemiennego w stanie ustalonym przeważnie pomija się część wskazu zależną od czasu, ponieważ jest ona taka sama dla wszystkich sygnałów napięć i prądów występujących w obwodzie. Co więcej, za moduł wskazu często w praktyce przyjmuje się nie amplitudę, lecz wartość skuteczną sygnału harmonicznego. Z tych właśnie powodów sensowym jest zdefiniowanie także wskazu niezależnego od czasu jako części stałej powyższego fazora, o module równym wartości skutecznej sygnału harmonicznego:
$$u = \frac{U_0}{\sqrt{2}}e^{j(\omega t +\varphi)} = \frac{U_0}{\sqrt{2}}e^{j\varphi}e^{j\omega t} \quad\Longrightarrow\quad U=\underbrace{\frac{U_0}{\sqrt{2}}}_{U_{sk}}e^{j\varphi}$$
Wskazy oraz ich wyprowadzenia zostały dokładnie omówione w kursie prądu przemiennego, polecam sprawdzić: Kurs prądu przemiennego.
Fazor zapewnia zatem prosty sposób przedstawiania wartości skutecznej (lub amplitudy) i fazy początkowej napięcia lub prądu przemiennego. Jest to liczba zespolona, której moduł i kąt (argument) odpowiadają wartości skutecznej (lub amplitudzie) i fazie początkowej sygnału AC. Wskaz zależny od czasu może być również użyty do reprezentowania amplitudy i fazy sygnału prądu przemiennego w dowolnym momencie.
Jedną z głównych zalet wskazów jest to, że można je dodawać, odejmować, mnożyć i dzielić tak jak zwykłe liczby, co pozwala na znaczące uproszczenie obliczeń wartości skutecznych (lub amplitud) i faz. Na przykład, jeśli dwa wskazy zostaną dodane do siebie, wynikiem jest nowy wskaz, który reprezentuje wypadkową wartość skuteczną (lub amplitudę) i fazę dwóch oryginalnych wskazów. Prostota rachunku fazorowego znacząco ułatwia analizę obwodów prądu przemiennego.
Czy wskazy są naprawdę przydatne?
Zapewne część z Was zastanawia się, do czego użyteczne są wskazy. Nie prościej by było po prostu liczyć wszystko za pomocą wzorów zapisanych w dziedzinie czasu? Spróbujmy odpowiedzieć na to pytanie, analizując prosty obwód RC. W praktyce inżynierskiej niejednokrotnie potrzebujemy obliczyć sumaryczne napięcie między zaciskami elementów połączonych szeregowo. Dobrym przykładem wydaje się pokazanie, ile czasu zajmuje obliczenie napięcia zastępczego, przy wykorzystaniu zarówno bezpośredniego rachunku, jak i wskazów. Obliczmy zatem napięcie na szeregowym połączeniu rezystora o oporności \(R\) i kondensatora o pojemności \(C\):
zakładając, że napięcie na rezystorze wynosi:
$$u_R(t) = 2\cos{\left(20t+135^\circ\right)}\ [{\rm V}]$$
a napięcie na kondensatorze
$$u_C(t) = 5\cos{\left(20t+45^\circ\right)}\ [{\rm V}]$$
Dodawanie napięć bez użycia wskazów
Napięcie na dwójniku będącym szeregowym połączeniem rezystancji \(R\) i pojemności \(C\) jest sumą napięć na rezystorze i kondensatorze:
$$u(t) = u_R(t) + u_C(t) = 2\cos{\left(20t+135^\circ\right)} + 5\cos{\left(20t+45^\circ\right)}$$
Obliczenie amplitudy i fazy początkowej tego napięcia będzie wymagało zapisania go za pomocą jednej funkcji trygonometrycznej. By to osiągnąć, skorzystajmy ze wzorów na cosinus sumy i różnicy dwóch zmiennych:
$$\begin{aligned}\cos{\left(\alpha + \beta\right)} &= \cos{\left(\alpha\right)}\cos{\left(\beta\right)}-\sin{\left(\alpha\right)}\sin{\left(\beta\right)}\\\cos{\left(\alpha -\beta\right)} &= \cos{\left(\alpha\right)}\cos{\left(\beta\right)}+\sin{\left(\alpha\right)}\sin{\left(\beta\right)}\end{aligned}$$
kładąc w nich:
$$\begin{cases}\alpha+\beta &= 20t + 135^{\circ}\\ \alpha-\beta &= 20t + 45^{\circ} \end{cases}$$
skąd możemy wyliczyć, że:
$$\begin{cases}\alpha &= 20t + 90^{\circ}\\ \beta &= 45^{\circ}\end{cases}$$
Wstawiając wyliczone \(\alpha\) i \(\beta\) do przytoczonych wzorów na sumę i różnicę kątów, otrzymamy
$$\begin{align*}\cos{\left(20t+135^\circ\right)} &= \cos{\left(20t+90^\circ\right)}\cos{\left(45^\circ\right)}-\sin{\left(20t+135^\circ\right)}\sin{\left(45^\circ\right)},\\ \cos{\left(20t+45^\circ\right)} &= \cos{\left(20t+90^\circ\right)}\cos{\left(45^\circ\right)}+\sin{\left(20t+\ 90^\circ\right)}\sin{\left(45^\circ\right)}.\end{align*}$$
Uwzględniając powyższe zależności w
$$u(t) = u_R(t) + u_C(t) = 2\cos{\left(20t+135^\circ\right)} + 5\cos{\left(20t+45^\circ\right)},$$
dostaniemy:
$$u(t) = P\cos{\left(20t+90^\circ\right)} + Q\sin{\left(20t+\ 90^\circ\right)}$$
gdzie \(P\) i \(Q\) oznaczają:
$$P = 7\cos{\left(45^\circ\right)} = \frac{7\sqrt{2}}{2}\qquad Q = 3\sin{\left(45^\circ\right)} = \frac{3\sqrt{2}}{2}$$
Otrzymany wzór pomnóżmy i podzielmy przez pierwiastek z sumy kwadratów \(P\) i \(Q\):
$$\sqrt{P^2+Q^2} = \sqrt{29}$$
w wyniku dostając:
$$u(t) = \sqrt{P^2+Q^2}\left(\frac{P}{\sqrt{P^2+Q^2}}\cos{\left(20t+90^\circ\right)} + \frac{Q}{\sqrt{P^2+Q^2}}\sin{\left(20t+\ 90^\circ\right)}\right)$$
dzięki temu, wprowadzając oznaczenia:
$$\begin{align}\cos{\left(\varphi\right)} = \frac{P}{\sqrt{P^2+Q^2}} = \frac{7}{\sqrt{58}}\\ \sin{\left(\varphi\right)} = \frac{Q}{\sqrt{P^2+Q^2}} = \frac{3}{\sqrt{58}}\end{align}$$
sumę napięcia na rezystorze i kondensatorze możemy zapisać jako:
$$u(t) = \sqrt{29}\left(\cos{\left(\varphi\right)}\cos{\left(20t+90^\circ\right)} + \sin{\left(\varphi\right)}\sin{\left(20t+\ 90^\circ\right)}\right)$$
W ostatnim przekształceniu skorzystamy ponownie ze wzoru na cosinus różnicy kątów, ostatecznie otrzymując:
$$u(t) = \sqrt{29}\cos{\left(20t + 90^\circ-\varphi\right)} \approx 5.39 \cos{\left(20t+66.8^\circ\right)}$$
Kąt \(\varphi\) może być obliczony za pomocą funkcji \({\rm arctan2}\) i w tym wypadku wynosi on:
$${\rm arctan2}(\sin{\varphi},\cos{\varphi}) = {\rm arctan2}\left(\frac{3}{\sqrt{58}},\frac{7}{\sqrt{58}}\right) \approx 23.2^\circ$$

Ufff… zadanie niby proste, ale trochę trzeba było się namęczyć. Teraz ten sam rachunek przeprowadźmy przy wykorzystaniu wskazów. Będziesz zdziwiony jak szybko można go wykonać dzięki nim.
Dodawanie napięć przy użyciu wskazów
Najpierw tworzymy wskazy niezależne od czasu odpowiadające napięciom chwilowym na rezystorze i kondensatorze:
$$\begin{align}U_R &= \frac{2}{\sqrt{2}}e^{j135^\circ}\\ U_C &= \frac{5}{\sqrt{2}}e^{j45^\circ}\end{align}$$
Dzięki wzorowi Eulera wskazy zapisane w postaci wykładniczej możemy przekształcić do postaci algebraicznej:
$$\begin{align}U_R &= \frac{2}{\sqrt{2}}\cos{\left(135^\circ\right)} +j\frac{2}{\sqrt{2}}\sin{\left(135^\circ\right)} = -1 + j\\
U_C &= \frac{5}{\sqrt{2}}\cos{\left(45^\circ\right)} +j\frac{5}{\sqrt{2}}\sin{\left(45^\circ\right)} = \frac{5}{2}+j\frac{5}{2}
\end{align}$$
Po dodaniu wskazów reprezentujących napięcie na rezystorze i kondensatorze otrzymamy wskaz:
$$U = U_R + U_C = \frac{3}{2} + j \frac{7}{2}$$
reprezentujący sumę napięć na rezystorze i kondensatorze. Pozostaje obliczyć jego moduł:
$$\left|U\right| = \left|\frac{3}{2} + j \frac{7}{2}\right| = \sqrt{\frac{29}{2}}$$
oraz jego argument:
$$\varphi = \arg{\left(\frac{3}{2} + j \frac{7}{2}\right)} \approx 66.8^\circ$$
Voilà, możemy już napisać wzór na napięcie chwilowe:
$$u(t) = \sqrt{29}\cos{\left(20t+66.8^\circ\right)}$$
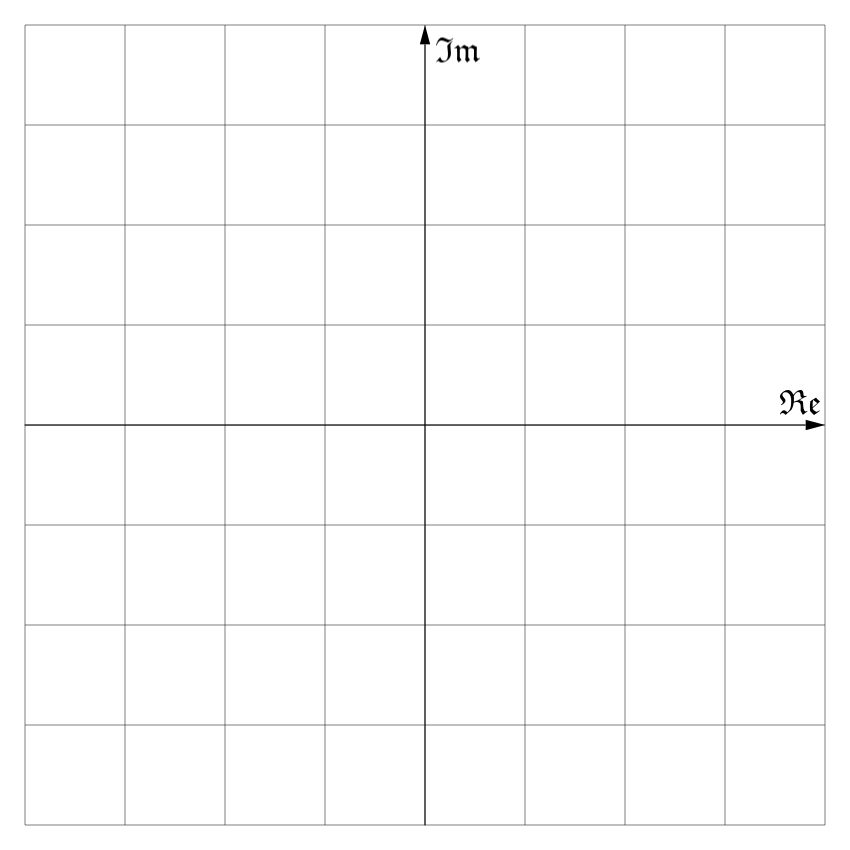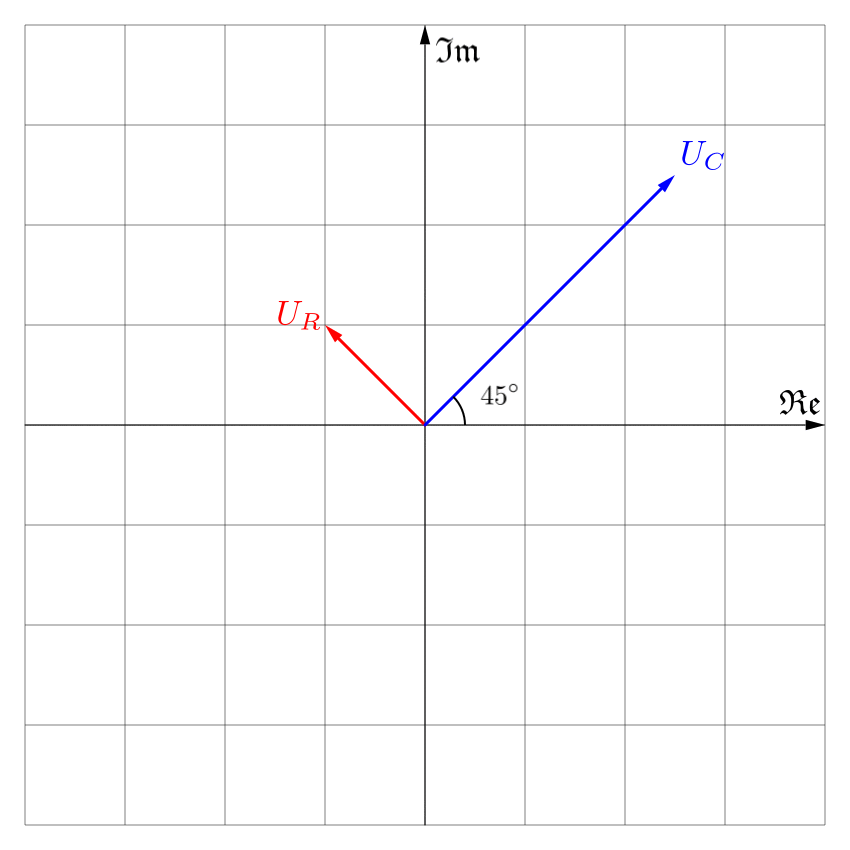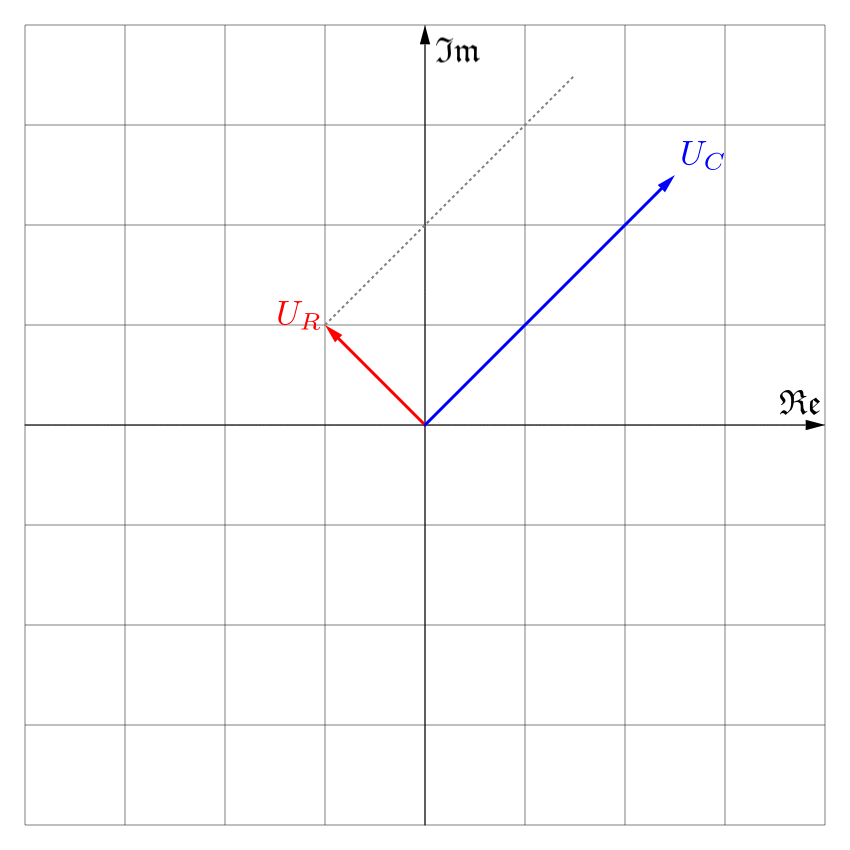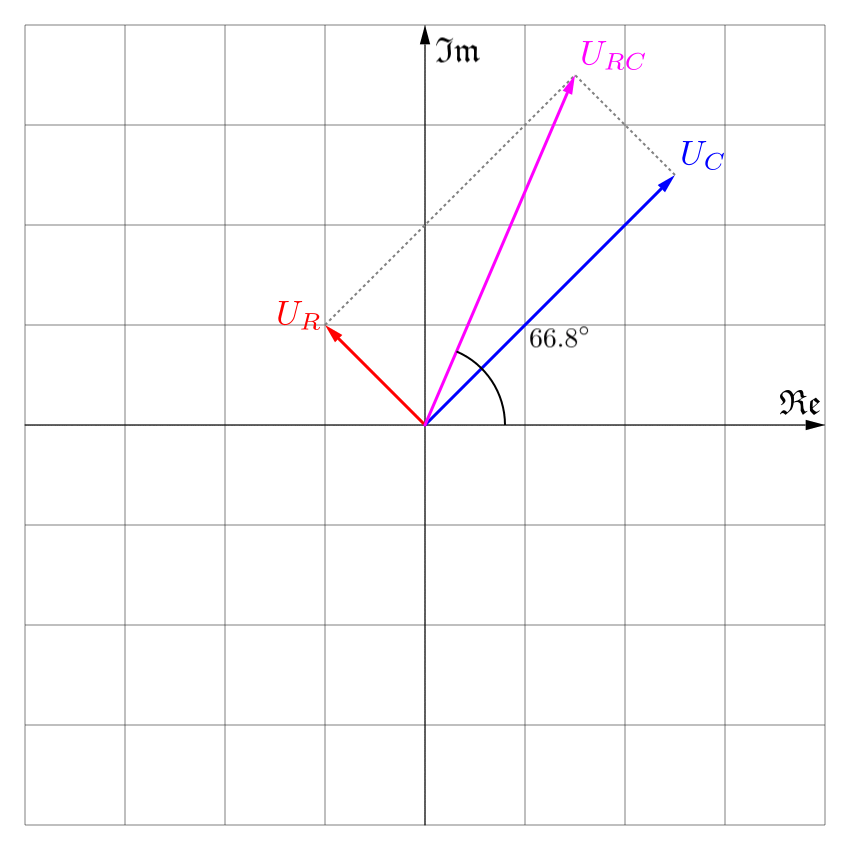
Jak widzisz rachunek przy użyciu fazorów jest zdecydowanie szybszy. Oczywiście wszystko przy założeniu, że pod ręką mamy urządzenie umiejące obliczać funkcje trygonometryczne, aczkolwiek bez niego nie nie obeszlibyśmy się i w pierwszym przypadku.
KURS PRĄDU STAŁEGO LUB PRZEMIENNEGO
Uczysz się elektrotechniki lub teorii obwodów? Prowadzący jest wymagający, ale nie potrafi dobrze przekazać wiedzy? Samodzielne przebijanie się przez tony wzorów i metod sprawia Ci duży problem?
Nie przejmuj się! Przygotowałem dla Ciebie programy, w których krok po kroku przeprowadzę Cię za rękę przez podstawy teorii obwodów.
Jeśli nie chcesz mieć problemów z dalszą nauką elektrotechniki, najpierw dobrze zrozum jej podstawy, czyli prąd stały. Warto ugruntować sobie tę wiedzę, ponieważ z pewnością wykorzystasz ją również w prądzie przemiennym, stanach nieustalonych, czy obwodach trójfazowych.
Zachęcam Cię do zapoznania się treścią kursów klikając w zdjęcia poniżej 🙂
Impedancja i moc pozorna to również wskaz!
Kolejną zaletą fazorów jest to, że można ich używać do przedstawiania zależności między sygnałami napięcia i prądu przemiennego w obwodzie. Na przykład relacja między wskazem reprezentującym napięcie w obwodzie a wskazem reprezentującym natężenie prądu jest również fazorem i leży u podstaw ważnych wielkości, takich jak moc pozorna i impedancja.
Dla osób chcących jeszcze bardziej zgłębić temat wskazów interesujący może okazać się artykuł o historii elektromagnetyzmu i elektrotechniki: A. E. A. Araújo · D. A. V. Tonidandel „Steinmetz and the Concept of Phasor: A Forgotten Story„.
Podsumowując, wskaz jest narzędziem matematycznym używanym do reprezentowania amplitudy i fazy początkowej napięcia lub prądu przemiennego. Jest to liczba zespolona, którą można dodawać, odejmować, mnożyć i dzielić jak zwykłe liczby, co pozwala na proste obliczenia w obwodach prądu przemiennego. Wskazy są zatem przydatnym narzędziem dla elektrotechników, którzy używają je do analizy i projektowania obwodów prądu przemiennego.





0 komentarzy