Każdy chyba słyszał, że napięcie w sieci elektrycznej to 230 V. Większość z nas wie również, że w gniazdku elektrycznym napięcie zmienna się naprzemiennie. Skąd zatem bierze się ta stała wartość 230 V? Dziś postaramy się to lepiej zrozumieć. Przyjrzymy się podstawowym parametrom opisującym przebiegi okresowe takim jak: okres lub częstotliwość, amplituda, wartość średnia i wartość skuteczna.
Wartość średnia przebiegu
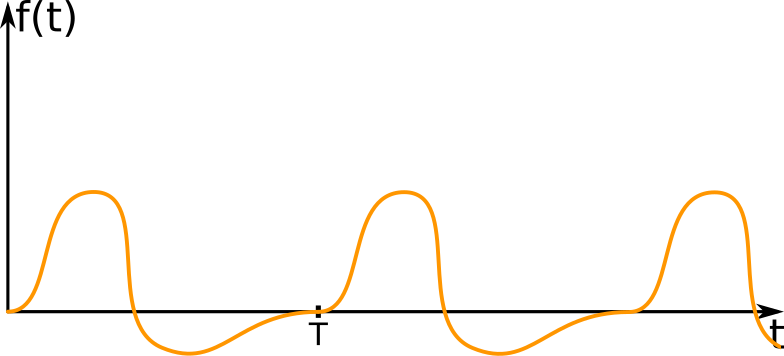
Wartość wokół, której oscyluje przebieg okresowy, nazywana jest wartością średnią. W przypadku przebiegów napięcia czy prądu wartość średnia nazywana jest również składową stałą odpowiednio prądu lub napięcia.
Do obliczenia wartości średniej przebiegu okresowego służy następujący wzór:
Zatem, aby obliczyć wartość średnią przebiegu, musimy wykonać całkę po przedziale o długości okresu i uzyskany wynik podzielić przez długość okresu.
Ponieważ mamy odczynienia z przebiegami okresowymi i całkujemy po przedziale o długości okresu, wybór chwili t₀, w której rozpoczynamy całkowanie, nie ma znaczenia dla ostatecznego wyniku. Najlepiej t₀ wybrać tak, żeby całkę było jak najłatwiej policzyć.
Przypomnijmy, że geometryczną interpretacją całki oznaczonej jest pole powierzchni między wykresem funkcji a osią czasu. Gdy wykres znajduje się nad osią czasu, pole powierzchni jest dodatnie, a gdy wykres znajduje się pod osią czasu, pole jest ujemne.
Zatem z geometrycznej interpretacji całki wynika, że przebieg stały w czasie równy wartości średniej innego przebiegu okresowego zakreśla w przeciągu okresu takie samo pole powierzchni co przebieg okresowy.
Napięcie średnie – trzy przykłady jak je policzyć
Wartość średnią możemy liczyć dla dowolnego przebiegu okresowego. Może być to wartość średnia napięcia, prądu, czy mocy. Obliczmy napięcie średnie dla kilku często spotykanych w praktyce przebiegów napięcia.
Przykład 1

W przypadku przebiegu prostokątnego, widocznego na powyższym wykresie, pole powierzchni pod wykresem przebiegu wynosi:

Dzieląc wynik całkowania przez okres, otrzymujemy, że napięcie średnie dla przebiegu prostokątnego nie zależy od T i jest równe:

Przykład 2

Równie łatwo obliczymy napięcie średnie dla przebiegu trójkątnego. Pole powierzchni pod wykresem tego przebiegu jest takie samo jak dla przebiegu prostokątnego i wynosi:

Po podzieleniu jego przez wartość okresu uzyskujemy napięcie średnie identyczne jak w poprzednim przypadku:

Przykład 3

W ostatnim przykładzie widzimy, że wkład dodatniego (pod wykresem i nad osią czasu) i ujemnego (nad wykresem i pod osią czasu) pola powierzchni jest identyczny, dlatego całka po okresie musi być równa zero.

Wyciągamy stąd wniosek, że napięcie średnie dla przebiegu sinusoidalnego jest równe zero.
KURS PRĄDU STAŁEGO LUB PRZEMIENNEGO
Uczysz się elektrotechniki lub teorii obwodów? Prowadzący jest wymagający, ale nie potrafi dobrze przekazać wiedzy? Samodzielne przebijanie się przez tony wzorów i metod sprawia Ci duży problem?
Nie przejmuj się! Przygotowałem dla Ciebie programy, w których krok po kroku przeprowadzę Cię za rękę przez podstawy teorii obwodów.
Jeśli nie chcesz mieć problemów z dalszą nauką elektrotechniki, najpierw dobrze zrozum jej podstawy, czyli prąd stały. Warto ugruntować sobie tę wiedzę, ponieważ z pewnością wykorzystasz ją również w prądzie przemiennym, stanach nieustalonych, czy obwodach trójfazowych.
Zachęcam Cię do zapoznania się treścią kursów klikając w zdjęcia poniżej 🙂
Wartość skuteczna przebiegu
Poza wartością średnią ważną dla przebiegów okresowych jest wartość skuteczna. Definicja wartości skutecznej, mimo iż wykorzystywana jest również w statystyce i teorii sygnałów, swój początek wzięła z teorii prądu przemiennego.
Wartość skuteczna natężenia (napięcia) prądu przemiennego jest taką wartością natężenia (napięcia) prądu stałego, która w czasie jednego okresu dostarczy do odbiornika taką samą energię co prąd zmienny.
Poniżej znajduje się definicja, którą wykorzystamy do wyliczenia wartości skutecznej przebiegu okresowego (prądu lub napięcia).

Podobnie jak wartość średnia, wartość skuteczna wyraża się przez całkę. Tym razem jednak całkujemy nie samo napięcie, lecz jego kwadrat, co powoduje, że wartość skuteczna, w przeciwieństwie do wartości średniej nie może być ujemna.
Możemy podsumować, że wartość skuteczna mierzy skuteczność okresowego przebiegu przemiennego prądu w dostarczaniu energii do odbiornika.
Napięcie skuteczne – trzy przykłady jak je policzyć
Obliczmy napięcie skuteczne dla kilku często spotykanych w praktyce przebiegów napięcia.
Przykład 1

Kwadrat przebiegu prostokątnego, potrzebny do obliczenia wartości skutecznej, możesz zobaczyć na poniższym wykresie.

Całkę w tym wypadku jest prosto obliczyć, ponieważ kwadrat przebiegu prostokątnego jest również przebiegiem prostokątnym. Możemy ją obliczyć podobnie jak w przypadku napięcia średniego.

Napięcie skuteczne dla przebiegu prostokątnego uzyskamy, biorąc z powyższego wyniku pierwiastek kwadratowy.
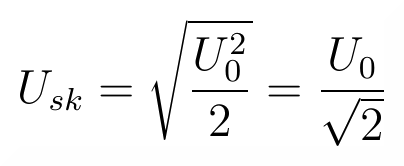
Przykład 2

Kwadrat przebiegu trójkątnego jest przebiegiem parabolicznym. Został on zilustrowany na poniższym wykresie.

Osoby zaznajomione z podstawami analizy matematycznej powinny zrozumieć poniższy rachunek, w którym została obliczona całka z kwadratu przebiegu trójkątnego.
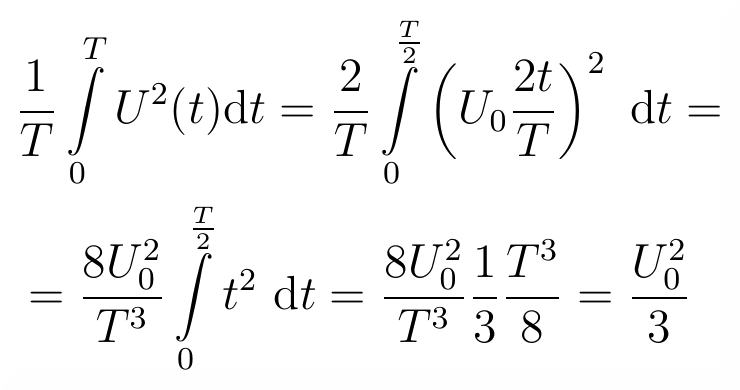
Wynik całkowania podzielony przez okres i spierwiastkowany daje następującą wartość napięcia skutecznego dla przebiegu trójkątnego:

Przykład 3

W ostatnim najbardziej praktycznym przykładzie wyliczymy napięcie skuteczne dla przebiegu sinusoidalnego. Kwadrat tego przebiegu możesz zobaczyć na poniższym wykresie.

Obliczenie pola powierzchni pod wykresem powyższej funkcji wymaga już biegłości w całkowaniu, dlatego poniżej bez szczegółowego omówienia został przedstawiony sam rachunek.

Wynik całkowania podzielony przez okres i spierwiastkowany daje następującą wartość napięcia skutecznego dla przebiegu sinusoidalnego:
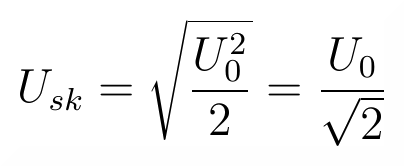
Napięcie skuteczne sieci energetycznej (jednej fazy) w Polsce wynosi 230 V. Z wyprowadzonej zależności możemy wyliczyć, że amplituda takiego przebiegu jest o pierwiastek z dwóch razy większa i wynosi aż U₀ = √2 · 230 V ≈ 325 V!





11 komentarzy
elektryk · 2021-01-20 o 22:53
Biorąc pod uwagę to że prawidłowe napięcie w sieci może wahać się +- 10% amplituda napięcia w sieci może osiągnąć nawet 357 V
Dariusz Szarejko · 2021-01-24 o 15:00
Jasne, Usk = 230 V to tylko w warunkach laboratoryjnych 🙂
Jacek · 2022-11-22 o 09:26
Jeżeli porazi mnie prąd z gniazdka domowego to zatrzęsie mną prąd o napięciu 230 czy 350 V
falconStrong · 2021-03-18 o 07:18
Hej.
Mam pytanie jakie jest napięcie skuteczne prądu przemiennego (dokładnie i = 10sin(100t)) na cewce, kondensatorze i rezystorze w obowddzie RLC oraz w obwodzie RL i RC? Czy to wylicza sie z tego samego wzoru Umaks/sqrt(2)?
Dziękuję =)
PS
Super artykuł. Bardzo przejrzysty =)
Dariusz Szarejko · 2021-03-18 o 11:50
Cieszę się, że artykuł się przydał 🙂
Co do pytania to: Jeśli elementy RLC, RL czy RC są połączone szeregowo to z grubsza tak. Żeby obliczyć wartość skuteczną napięcia na elemencie, trzeba pomnożyć zawadę tego elementu (R, ωL, 1/(ωC), ω=100) przez wartość skuteczną natężenia prądu (I_max/√2 = 10 / √2 [A]), który przepływa przez ten element (R, L lub C).
Xenon · 2021-11-09 o 01:11
A przy sygnałach prostokątnych wartość średnia sygnału nie zależy też od współczynnika wypełnienia? Czy tylko ja się tutaj mylę?
Dariusz Szarejko · 2021-11-09 o 09:49
Tak, zależy 🙂 W artykule przyjąłem, że współczynnik wypełnienia sygnału prostokątnego jest stały i wynosi 50 %.
Szymon · 2021-11-28 o 20:08
Mam pytanie. Mając za zadanie obliczyć średnią wartość napięcia z wykresu trójkątnego przemiennego gdzie aplituda górna jest lekko różna od dolnej, mam podać za wartość ich różnicę dzieloną przez 2? czy jak to wygląda? jak obliczyć niepewność pomiarową?
Dariusz Szarejko · 2021-11-28 o 23:03
To o czym piszesz to prawdopodobnie sygnał trójkątny ze składową stałą. Wartość średnia takiego sygnału jest połową sumy napięć minimalnego i maksymalnego 🙂 Na resztę pytań nie jestem w stanie odpowiedzieć.
Karol · 2023-07-17 o 13:45
Zdaje się, że w definicji wartości skutecznej jest błąd.
Jest: „(…)dostarczy do odbiornika taką samą energię co prąd zmienny”;
a powinno być : „(…)dostarczy do odbiornika taką samą energię co prąd stały” .
Dariusz Szarejko · 2023-07-17 o 18:25
Definicja jest poprawna. Musimy sobie wyobrazić, że mamy dwa źródła jedno stałe „A” a drugie przemienne „B”. Oba te źródła „A” i „B” zasilają przez czas T identyczne odbiorniki rezystancyjne.
Wartość napięcia stałego źródła „A” będzie równa wartości skutecznej źródła przemiennego „B”, kiedy źródło stałe „A” dostarczy do odbiornika rezystancyjnego taką samą ilość energii co źródło przemienne. Inaczej mówiąc, w obu przypadkach skutek energetyczny będzie identyczny.