Przekształcenie gwiazdy w trójkąt (lub trójkąta w gwiazdę), nazywane również transfiguracją gwiazda-trójką (lub trójkąt-gwiazda) znajduje szczególne zastosowanie w układach trójfazowych. Warto rozumieć skąd się ono bierze i na czym polega. Dziś przyjrzymy mu się nie co dokładniej od strony teoretycznej.

Wyprowadzenie wzorów na transfigurację

Układ elektryczny, który ma trzy zaciski (inaczej mówiąc „ma trzy nóżki”) nazywamy trójnikiem.
Połączenie trzech elementów w gwiazdę lub trójkąt jest zatem trójnikiem, ponieważ w wyniku takiego połączenia uzyskujemy układ posiadający trzy zaciski elektryczne.
Załóżmy teraz, że mamy trzy rezystory o znanej rezystancji (lub ogólniej trzy impedancje) połączone w trójkąt. Następnie zamknijmy ten układ w czarnej skrzynce w taki sposób, żeby na zewnątrz wychodziły tylko trzy zaciski A, B, C. Podobnie postąpmy w przypadku układu trzech innych rezystorów połączonych w gwiazdę. Zamknijmy go w czarnej skrzynce, w taki sposób na zewnątrz wychodziły tylko trzy zaciski A, B, C.
Zachodzi teraz pytanie, czy możliwe jest takie dobranie wartości rezystorów (lub impedancji) połączonych w gwiazdę, żeby oba układy były równoważne elektrycznie? Inaczej mówiąc, czy jest możliwe, żeby układów nie dało się rozróżnić bez zaglądania do środka czarnych skrzynek?
Przypomnijmy, że układy elektryczne nazywamy równoważnymi elektrycznie jeżeli do układów wpływają te same prądy jeśli do ich zacisków przyłożymy do nich identyczne napięcia.
Odpowiedź brzmi: Tak, Jest to możliwe! Wystarczy, żeby każda para zacisków w obu układach posiadała tę samą rezystancję (lub w ogólnym przypadku impedancję).
W przypadku połączenia w gwiazdę rezystancja między zaciskami A i B jest sumą oporów Ra i Rb natomiast rezystancja między zaciskami A i B w połączeniu w trójkąt jest równa równoległemu połączeniu rezystorów Rab wraz z sumą Rbc i Rca. Spróbujmy zapisać to równaniami. W przypadku równoważności zacisków AB:
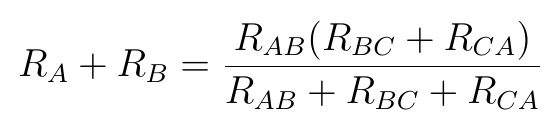
Analogiczną zależność otrzymamy w przypadku porównania rezystancji widzianych z zacisków BC:
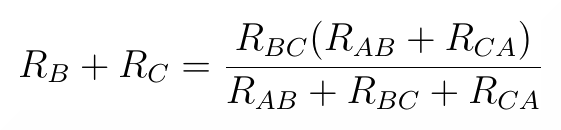
oraz w przypadku porównania rezystancji widzianych z zacisków CA:
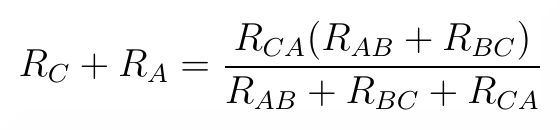
Po obustronnym zsumowaniu trzech otrzymany zależności i podzieleniu przez dwa, otrzymamy równanie:
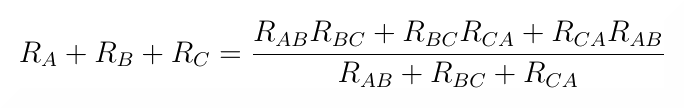
KURS PRĄDU STAŁEGO LUB PRZEMIENNEGO
Uczysz się elektrotechniki lub teorii obwodów? Prowadzący jest wymagający, ale nie potrafi dobrze przekazać wiedzy? Samodzielne przebijanie się przez tony wzorów i metod sprawia Ci duży problem?
Nie przejmuj się! Przygotowałem dla Ciebie programy, w których krok po kroku przeprowadzę Cię za rękę przez podstawy teorii obwodów.
Jeśli nie chcesz mieć problemów z dalszą nauką elektrotechniki, najpierw dobrze zrozum jej podstawy, czyli prąd stały. Warto ugruntować sobie tę wiedzę, ponieważ z pewnością wykorzystasz ją również w prądzie przemiennym, stanach nieustalonych, czy obwodach trójfazowych.
Zachęcam Cię do zapoznania się treścią kursów klikając w zdjęcia poniżej 🙂
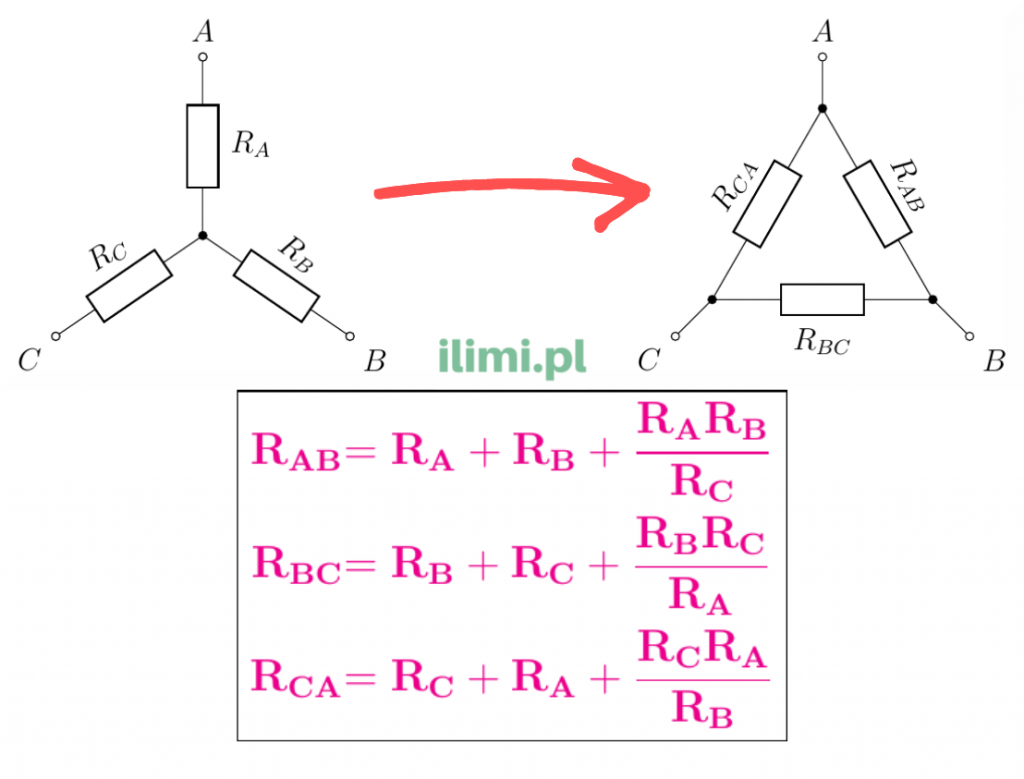
Zamiana trójkąt-gwiazda
Wzory na transfigurację trójkąta w gwiazdę otrzymamy po odjęciu stronami od ostatniego równania kolejno równania 3, 2, 1:

określające wartości rezystancji Ra, Rb, Rc elementów trójnika połączonego w gwiazdę równoważnego trójnikowi połączonemu w trójkąt.
Zamiana gwiazda-trójkąt
Związki odwrotne otzymamy jeżeli następującą sumę iloczynów (obliczoną za pomocą wzorów 5, 6, 7):

podzielimy kolejno stronami przez równania 7, 6, 5. Otrzymamy wtedy zależności na przekształcenie gwiazda-trójkąt:





0 komentarzy